澳门认证✔九游娱乐【2024欧洲杯】
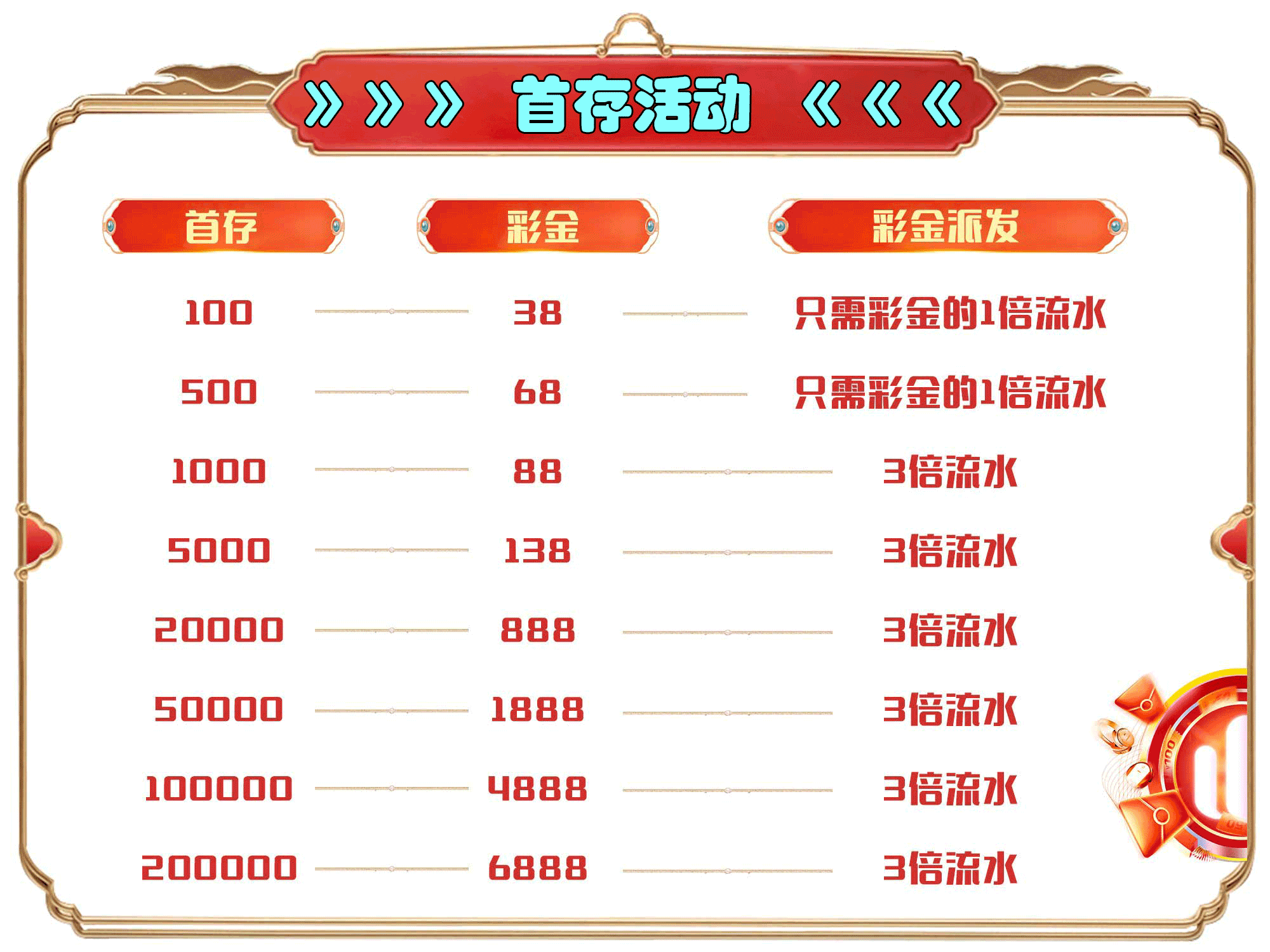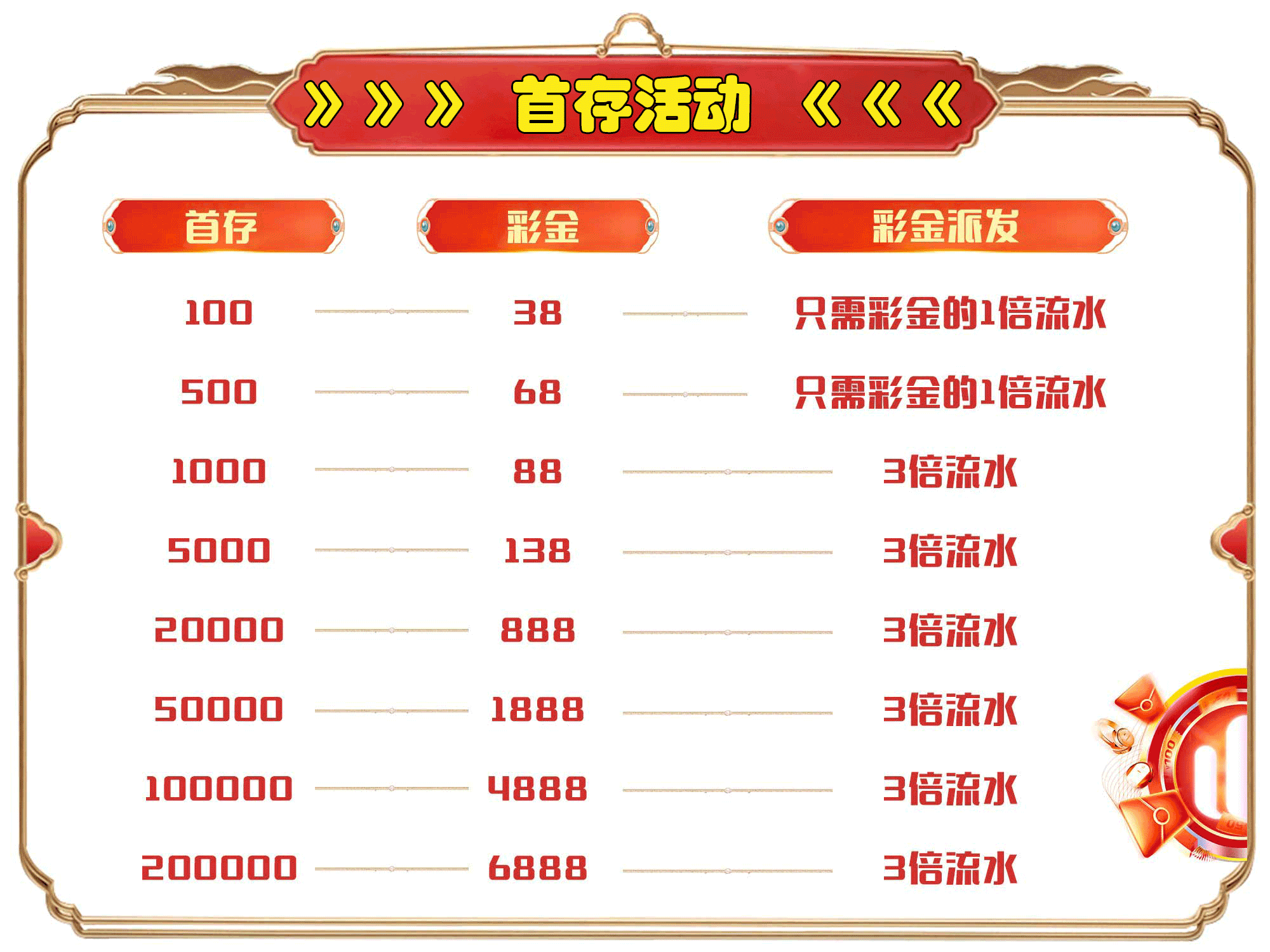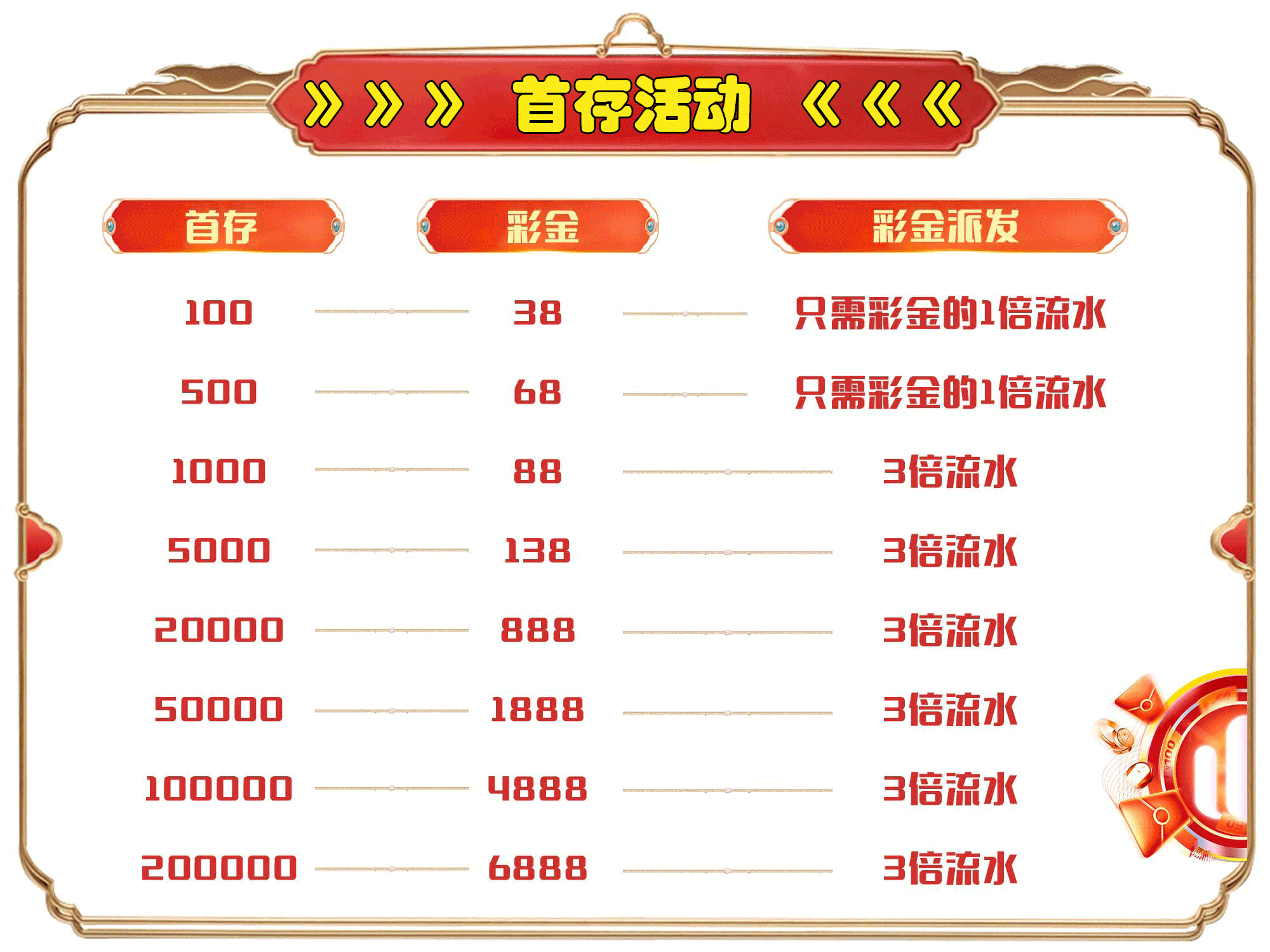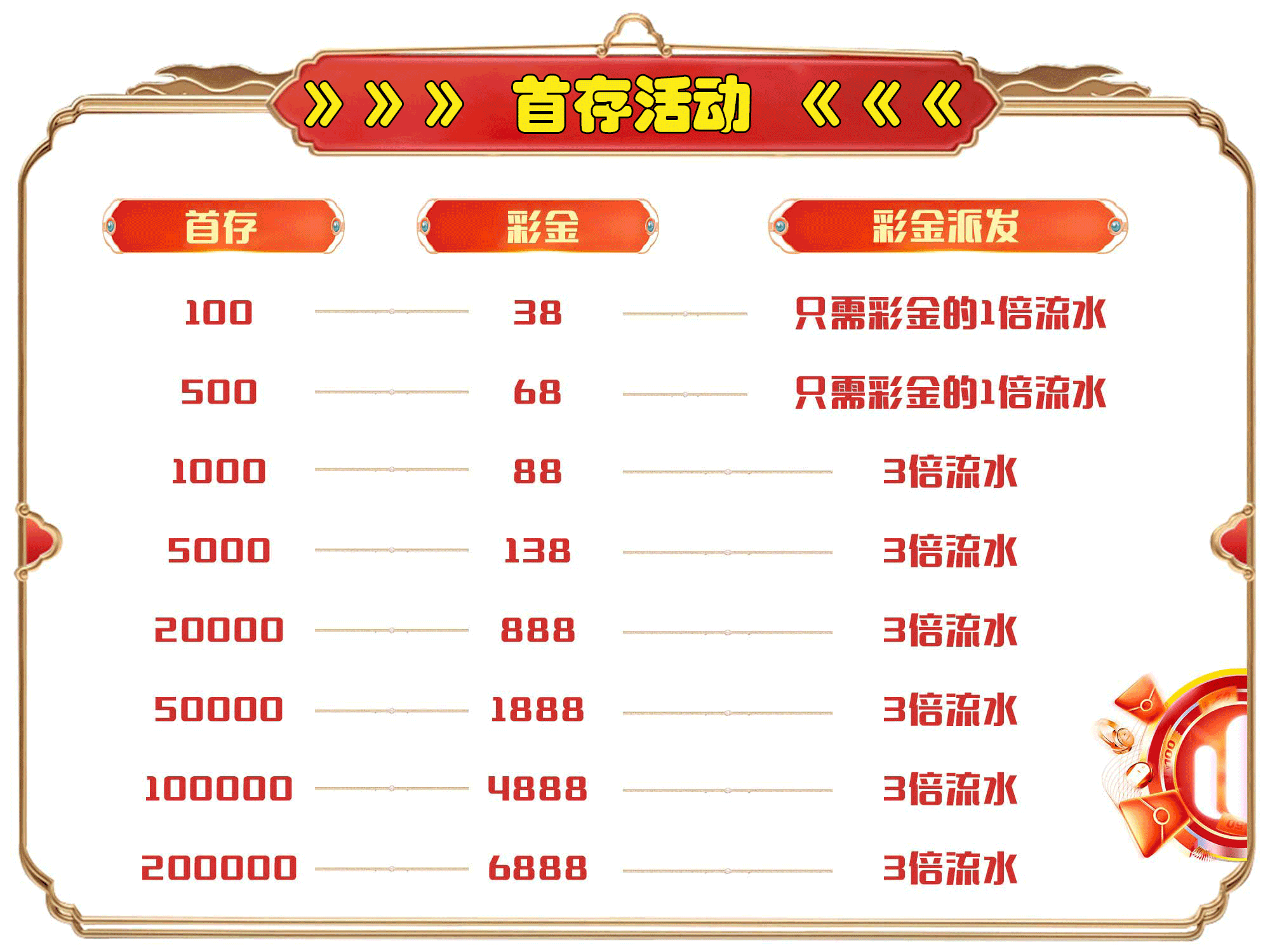
🔥首存100赠送38! 无限活动!
🔥首充即送! 高达6888元!
🔥大额无忧 豪客首选 | 单日取款无上限
- ·真人视讯
- ·电子游戏
- ·体育投注
- ·彩票棋牌
- ·电竞投注
- ·电子娱乐
九游棋牌官网
- 最专业棋牌品牌 尽享满冠
▶
星空娱乐官网
- 最高返水1.20%🔥
- 澳门官方直营品牌
▶

九游体育全站APP
安全、最快的存款和取款 点击进入
超高返利带您玩转真人视讯
完成新手任务好礼等您来

星空娱乐全站APP
美女主播在线畅聊
红单推荐赛事分析晒单功能精彩连麦
多元化的玩法 投注赛事